We are sometimes given a vagina—and that designates a “woman”—virgin, bride, etc.—and sometimes a penis—and that indicates a “man”—bachelor, groom, etc. This physiological accident was never anything more than the effect of an assuredly ironic causality: the laws of Euclidian geometry. In a four-dimensional study … vagina and penis, like an anamorphic illusion, would immediately lose all distinctive character. It is the same object that we would sometimes see as “male” and sometimes as “female,” in this perfect mirror-like reversal of the body that presupposes, because it takes place, the existence of a fourth dimension.
—Jean Clair, Sur Marcel Duchamp et la Fin de l’Art
Enantiomorphs and Kant
An object that has a length has one dimension. A length and width make two, and an object with a length, a width, and a height has three dimensions. Any object that really exists, from the time it came into existence until the moment it vanishes forever, has duration, the fourth dimension. Before the fourth dimension began to be treated as time, however, it was briefly described as a transcendental dimension of space and imagined as the domain of whatever way of being in extension came after height.
The possibility of higher-dimensional space is often traced to the twenty-four-year old Immanuel Kant, who speculated, in Thoughts on the True Estimation of Living Forces (1747), that “if it is possible that there are extensions with other dimensions, it is also very probable that God has somewhere brought them into being; for His works have all the magnitude and manifoldness of which they are capable.” He later returned to this thought in The Prolegomena to Any Future Metaphysics (1783), where, in a puzzling little paragraph, he asks himself: If all space were empty but for a single human hand, would it make sense to ask whether that hand was specifically a right hand?1
To visualize the problem Kant posed, imagine the outline of a hand printed onto a transparent surface. It can appear to be either a left or a right hand, depending on the position of the observer. Left or right only make sense within the boundaries of two-dimensional space; once you move into the third dimension, left and right become observer-dependent, rather than independent, characteristics. Their outline is neither left nor right, but sometimes left and sometimes right.
This is because right and left hands are identical but asymmetrical. Kant called these objects “incongruent counterparts,” known in geometry as enantiomorphic objects. Enantiomorphs are objects whose geometrical properties are exactly alike, but which are not congruent: were one to move a right hand onto the left-hand position, the two wouldn’t match. The thumb would always be found on the opposite side. Though this might seem trivial, for Kant enantiomorphs were tied to the very nature of space. Were one to insert a handless body into the space that contains only a single hand, our perception would radically change: clearly the severed hand would not fit onto either wrist; it would fit only either the right or the left one. Say it fits the right wrist, does that mean it was a right hand all along?
Prior to Kant, Leibniz had argued that “space has no reality apart from material things; it is nothing more than an abstract, mathematical description of relations that hold between objects.”2 Space is the order of the coexistence of bodies, just as time is nothing other than the order of the succession of events. Kant was however persuaded that the existence of “incongruent counterparts” pointed to a different perspective: space is absolute, and it determines, instead of being determined by, the objects inside it.3
It wasn’t until 1827, eighty years after Kant published his initial paper on “living forces,” that August Ferdinand Möbius realized that since adding depth to the plane allowed for a two-dimensional hand to be flipped over by rotating it around an axis, in a forth dimensional space a three-dimensional hand could likewise be “turned over,” e.g., reversed from a left hand to a right one.4 Möbius imagined the move to four dimensions as analogous to the move from two dimensions to three, in effect generalizing the rules of three-dimensional Euclidean space to include the hypothetical fourth dimension. The canonical objects for these rotations are the Möbius strip (a paradoxically unisurficial and unilateral volume) and the Klein bottle (named after Felix Klein, the Klein bottle is constructed by joining the edges of two Möbius strips, and has neither an inside nor an outside). If a flat being walks along a Möbius strip, his innards will reverse themselves, and he will end up with his heart on the right-hand side; a snail whose shell spirals counterclockwise would find it reversed to clockwise by the end of its stroll.

In 1846, spatial speculation went further when the physicist and experimental psychologist Gustav Theodor Fechner made the existence of a fourth dimension comprehensible to a wider audience. His essay “Der Raum Hat Vier Dimensionen” (published under the pseudonym “Dr. Mises”) proposed a dimensional analogy: the reader is asked to imagine how one would explain the third dimension to a shadow-like being inhabiting a flat, two-dimensional world. The shadow-man, Fechner argued, would likely perceive a third-dimensional being as some sort of motion. Imagine a sphere intersecting a plane: the flat creatures who inhabit said plane cannot possibly conceive of a three-dimensional thing such as a sphere. Instead, the sphere’s transit appears as a series of circles increasing and then decreasing in size. Two dimensional beings would thus mistake the third dimension for a temporal phenomenon––as a sequence of multiple two-dimensional objects rather than the movement of a single three-dimensional one. In an analogous manner, Fechner reasoned, we three-dimensional creatures are unable to grasp the fullness of a four-dimensional being, and are likely to make the same mistake as our shadow counterparts, misrecognizing the morphology of fourth-dimensional beings as a kind of motion and identifying it with time.
Such arguments for a spatialized fourth dimension were enabled by the development of non-Euclidian geometries and n-dimensional space. Although Möbius had given the physical properties of four-dimensional objects a solid mathematical grounding, non-Euclidian geometries do not necessarily imply a fourth, Euclidian dimension comparable to the initial three.5 As physicist Hermann von Helmholtz noted, the “so-called measure of space curvature is a quantity obtained by pure analytical calculation and its introduction involves no suggestion of relations that would have a meaning for sense perception.”6 Whereas Helmholtz, mathematician Bernhard Riemann, and Bertrand Russell treated the fourth dimension as an algebraic variable of analytic geometry, fourth-dimension enthusiasts instead spread the gospel of the fourth dimension as a generalization of Euclidian space. Like other such breakthroughs, these discoveries soon migrated outside the realm of science to be popularized, moralized, and personified by mystics, visionaries, and writers.
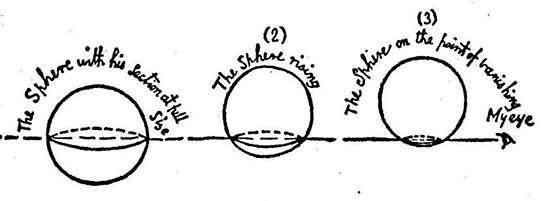

Specters From the Fourth Dimension
The nature of space is not simply a physical question, but a metaphysical one. Once a consensus had been reached that space is infinite and thus, by necessesity, homogenous, the question becames where to place God. He cannot be inside space, since the creator cannot be lesser than the creation. But nor can he be outside space, since space is infinite. Arguing against the idea of God as supra-mundane intelligence, but also not willing to identify Him with space, Newton proposed that space is God’s sensorium, the organ which God makes use of to perceive things. Though Newton later backtracked,7 in the nineteenth century the residual belief in the “world soul” would experience a revival, reinforced by the surge of interest in Buddhism and Hinduism.
Not only God was left homeless by Newtonian physics: once space becomes homogenous, spirits and specters are also forced to assume properties within the jurisdiction of the laws of physics. The materialization of psychic phenomena was a widespread obsession in late-nineteenth-century occult circles. Around the 1870s, a plethora of psychics claimed the ability to act as conduits or transmitters; much like a human radio frequency receiver, they could allegedly capture cosmic vibrations that were said to manifest in a fashion similar to electromagnetic waves. In the 1880s Oliver Lodge linked “psychical phenomena such as telepathy, telekinesis, and ectoplasm” to the ether, “speculating that electrical and psychical manifestations were linked phenomena that described the deeper underlying structures of the universe, beneath and beyond matter.”8 Like the ether, ectoplasm can be at times a medium, at times a substance—these metamorphic entities are, one could say, analogues for money, which itself had been transforming rapidly between a medium of exchange and a commodity form since the panic of 1873. The wave theory of light also presupposed the existence of a medium in which the light waves could propagate, leading both Thomson (Lord Kelvin) and Maxwell to treat “the electromagnetic field as the product of the structure and motions of an underlying mechanical ether.”9 The field of physiology dealt with telepathy and telekinesis, and there was no clear distinction between the scientific domain of neurophysiology, the emergent field of electromagnetic technologies, and the para-scientific circles of esoteric beliefs and séance gatherings.
Influenced by Fechner’s ideas, Johann Karl Friedrich Zöllner, the chair of astrophysics at Leipzig University—the same place where Möbius taught––came to the conclusion that spirits were in reality four-dimensional beings, whose existence could only manifest itself partially. Zöllner was fascinated by the American medium Henry Slade’s (alleged) ability to tie and untie knots in a cord whose ends had been previously sealed with wax—a deed which, in Zöllner’s view, proved that the fourth dimension was real. Zöllner hypothesized that spirits could turn a three-dimensional object into its mirror image by means of a rotation in four-dimensional space. He had Slade conduct séances under laboratory conditions in which Slade attempted to turn the clockwise spiral on snail shells counterclockwise, remove a coin from a locked container, and interlink rings. Wilhelm Wundt, the psychologist who Zöllner had invited as an observer, felt immediately suspicious of the ghost’s poor grasp on German grammar.10 Slade also failed to invert the snail’s spiral. None of this affected Zöllner’s belief in four-dimensional beings, however. Nor did the fact that Slade had been tried for fraud in 1876, or that his tricks were exposed by the Seybert Commission in 1885.11 Zöllner was unwavering, and mobilized his colleagues in Slade’s defense. When fellow scientists began to scrutinize his séances, Zöllner accused Wundt of being possessed by evil spirits. The debunking of Slade’s hoax also did not dent the growing public appeal of the fourth dimension, and literature on the subject proliferated in inverse proportion to its scientific credibility.


The Fourth Dimension as Social Metaphor
While the dimensional analogy argument seemed compelling, higher dimensions didn’t readily lend themselves to pictorial representation. Though Ludwig Schläfli had discovered six higher-dimensional regular polyhedra in 1852, he worked algebraically: without any means to visualize these figures, his readership was unfazed. To envision the fourth dimension remained virtually impossible. Like capital, whose magnitude cannot be observed or quantified directly, only revealing itself through the price system, the fourth dimension only reveals itself indirectly.
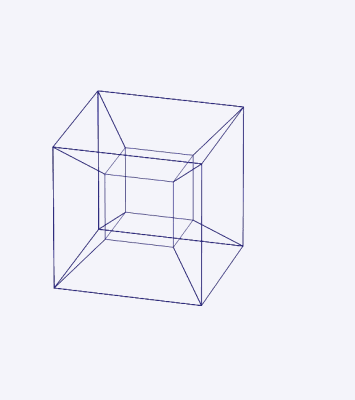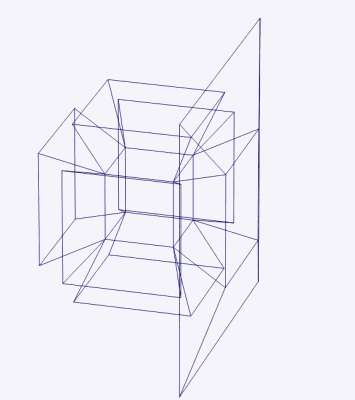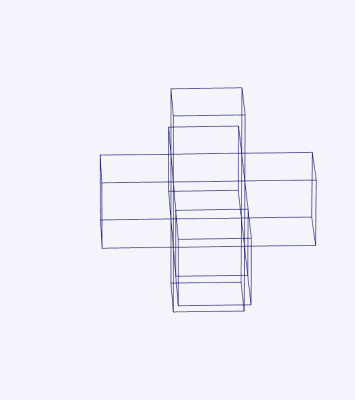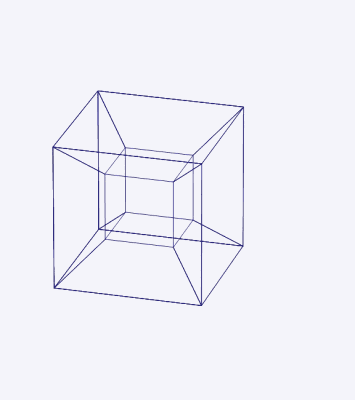
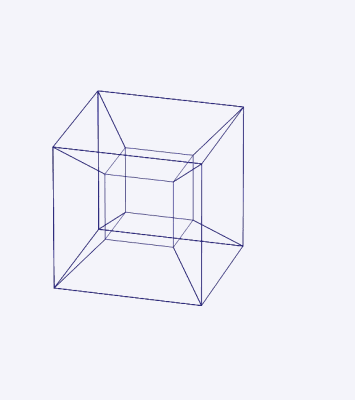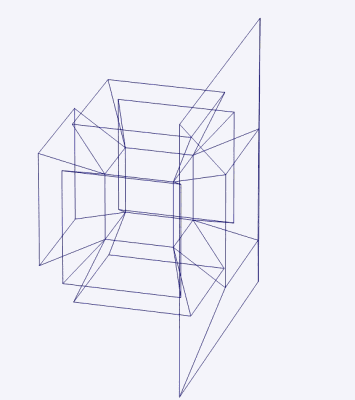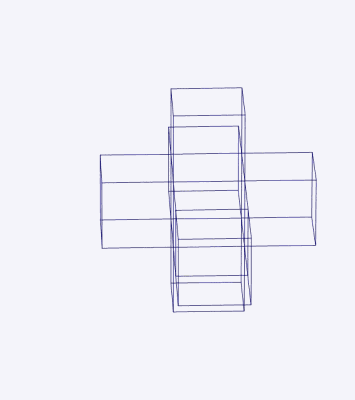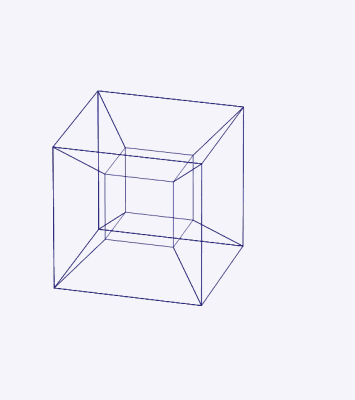
This can perhaps account for the success of “What is the Fourth Dimension?,” an 1880 article by the mathematician and science fiction author Charles Howard Hinton, which was subsequently reprinted nine times. Hinton recognized that it would be impossible to grasp the forth dimension directly, and so he introduced a system of colored cubes—the study of which, he claimed, made it possible to train the mind to visualize four-dimensional space. Following Hinton’s method, “we are to see the sections of the tesseract as they pass through our space, and the patterns of changing colors are means of recognizing the position of the tesseract and its component cubes at any moment.”12
That same year, W. I. Stringham published “On Regular Figures in N-Dimensional Space,” an article containing one of the earliest known illustrations of the projections on a plane of the six regular polyhedroids or polytopes—the four-dimensional counterparts of the five regular polyhedra.13 Like Hinton, Stringham worked synthetically; unlike Hinton however, he did not equate higher mathematical dimensions with heightened states of consciousness.14 In later works (such as “Casting out the Self” and A New Era of Thought), Hinton argued that in order to access the higher order of being occluded by Euclidian space, one must cast out the self, i.e., get rid of both one’s familiar spatial coordinates (left/right, up/down) and one’s sense of personhood by identifying with another person. Building on Thomson’s vortex theory, Hinton also suggested that electrically charged particles are kinds of four-dimensional enantiomorphs or mirror images, which appear at times positive and at times negative because space warps around the unseen fourth dimension: what appears as a physical force—attraction and repulsion in the case of electromagnetism—is an effect of geometrical properties.15 This important insight foreshadowed Theodor Kaluza’s observation that the fundamental forces of physics can be unified by the introduction of higher spatial dimensions.16
Hinton’s method was found wanting, however. A reader called the autohypnotic process “completely mind-destroying,” and rumors subsequently arose that Hinton’s cubes could drive unsuspecting gentlemen insane.17 In an unrelated twist of fate, Hinton was convicted of bigamy for marrying both Mary Ellen Boole (daughter of Mary Everest Boole and George Boole, the founder of mathematical logic) and Maud Florence Weldon. In 1885 Hinton served three days in prison, thereafter leaving England in a self-imposed exile.
The fourth dimension also had no shortage of detractors. In Alice in Wonderland and Through the Looking Glass (written under the name “Lewis Carroll” for fear of reprisals), Charles Dodgson mercilessly mocked the novel mathematical ideas which, he felt, opened up a slippery slope between the language of algebra and that of geometry, endowing algebraic variables with the semblance of concrete existence.18 In Euclidean geometry, mathematical objects are conceived as the ideal representation of their physical counterparts. Euclid believed that the problem of the universal applicability of a method was the problem of the universality of the mathematical objects themselves. Post-Cartesian mathematics, on the other hand, “identifies the object represented with the means of its representation and it replaces the real determinateness of an object” with a sign which “signifies possible determinacy.”19 The function of such signs is to establish a relation between that object and the overall system of mathematical objects. The objects themselves exist only through such relations. The fourth dimension, Carroll argued, was a case of the hypostatization of language: abstraction taken literally, and set phrases, metaphors, and figures of speech given concrete reality.20
In his review of “What is the Fourth Dimension?” Bertrand Russell also accused Hinton, whom he called a “conscientious bigamist,” of claiming that “our three-dimensional world is superficial,” in a manner which blended “the common and the mathematical meaning of this adjective,” thus equivocating social grievances and spatial properties.21
Objections notwithstanding, the reification of language––owing to the outright identification of the mental with the transcendental—became the hallmark of Victorian theory. According to Thought-Forms (1901) by the Theosophists Annie Besant and Charles Leadbeater, “thoughts are things,” and as such, they can manifest as visible auras. The Theosophical concept of “astral vision” was, in Leadbeater’s view, akin to a form of four-dimensional sight, and he equated the Theosophical doctrine of higher planes of consciousness with higher-dimensional space, the “astral plane.”22
The belief in metamorphic entities which only reveal themselves partially, and the description of matter existing at what Leadbeater would call varying degrees of “tenuity,” mirrors the Marxist description of an object-world whose familiar appearance is nothing but a distortion of the static bourgeois gaze. Like atoms whose vortices are the visible motions of an invisible ether, the object-as-commodity is the visible tip of an invisible whole. Capitalism is a multidimensional force whose properties can only be grasped sectionally. Much like the fourth spatial dimension is misrecognized as time, the intersections of the inscrutable flows of capital with the social body are misrecognized as a sequence of micro-pressures rather than the movements of a single, titanic pull.
Higher-dimensional theory and Theosophy tend to share with socialism a disaffection with the rigidity of social norms, roles, and protocols. Unlike socialism, however, speculation about higher dimensions or astral vision tends to misrecognize societal constraints as spiritual hindrances, thus preventing social tensions from taking a political form.

But the fourth dimension has a political unconscious. In Edwin Abbott’s satirical novel Flatland: A Romance of Many Dimensions (1884), the social anxieties lurking in higher-dimensional speculation are all made manifest. In Flatland, social restrictions are expressed as spatial limits. The flat universe is a caste society in which social ranking follows from geometric shape: the more sides to a polygon, the higher its ranking. Women are simple lines, and social mobility is strictly regimented, allowing the polygons to ascend the social ladder only one generation at a time. Potential working class leaders are either promoted or eliminated. Flatland is a scathing critique of Victorian England’s punitive polity and rigid class divide. In a society shaped by glaring asymmetries and uneven development, economic insecurity was swiftly systematized into a code of conduct, making coercion from without appear as coercion from within.
At the same time, the novel also became the major vehicle for the dissemination of the dimensional analogy. By describing a fantastic world of flat beings (like squares and circles) for whom three-dimensional forms (like spheres and cubes) seem supra-natural, Flatland proposed a logical sequence: lineland—flatland—spaceland. The analogy is then extended to account for our own awe at the thought of four-dimensional beings who are able to see our innards much the same way that we are able to see the inside of a circle, and who are endowed with the power to turn our bodies over with the same easy with which we flip geometrical figures around an axis. And what would it be like to be turned over in the fourth dimension? Well, you’d rotate around a plane that cuts through your body—through the tip of your nose, through your navel, and through your spine. While that plane would stay in our own three dimensional space, the rest of you would swing past the rotation plane, through the fourth dimension, and onto your mirror image. Think of a right-hand glove turned inside out: it now fits your left hand instead.

Enantiomorphs and Lacan: The Fourth dimension as Sexual Phantasm
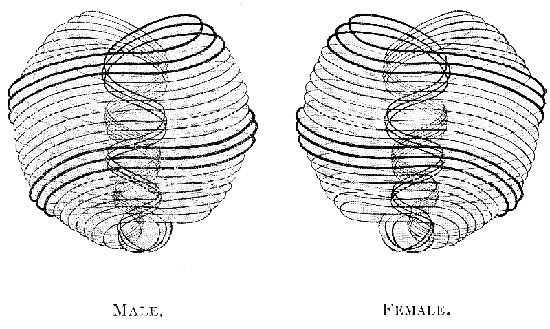
The fourth dimension was also tied up with a definition of gender, as a geometrical ideal which abolishes sexual differentiation. Male and female can be construed as four-dimensional enantiomorphs, whose division is a distortion of the limited three-dimensional gaze bound by the laws of Euclidian geometry. In a four-dimensional space the notion of a distinct gender would lose all specificity, and an object would sometimes appear as male, sometimes as female, depending on the observer’s position. As Jean Clair—who described Marcel Duchamp’s Dart Objects as a representation of fourth-dimensional genitalia—observes, this reversability of organs, like the structure of a glove turned inside out, would point to the fact that “the penis and vagina are a single organ, one and the same—an otherwordly organ, a Mélusinian organ,” and that “the genitals, seen as truncated, like the division of the being from itself—like a lack—is merely the effect of three-dimensional space.”23
In Victorian England, the female body depended upon the male body for its definition, anatomically as well as politically,24 and metaphors of inversion structured the rhetoric of fields as diverse as medicine and morals, reflecting a broader tension between inner and outer. The quivering masturbator, for instance, emerged as a disruptive figure because masturbation directs sexuality “inwards,” towards nonreproductive ends. Meanwhile,in medical and forensic science, female anatomy was seen as a reversal of male anatomy. “The female was the male, turned outside in, retaining in her body the organs that, properly developed, were necessarily outside. Thus the ovaries were called ‘female testicles’ … The vagina was the penis; the uterus the scrotum.”25 The female is, as it were, a mutilated male.
Between September and October 1888, the serial killer known as Jack the Ripper murdered five women in such a gruesome and brutal way that his crimes received unprecedented coverage in the media. Violent sexual attacks were not uncommon in Victorian London (in fact, two other victims were initially added to the Ripper’s tally, so high was the murder rate in Whitechapel), but none looked like these. According to the forensic notes made by Dr. Thomas Bond, the perpetrator cut the women’s throats and sliced the tissue of their necks down to the bone, then divided their bodies along an axis, from chin to pelvis, before removing the whole surface of the abdomen and extracting its viscera. Distressed policemen said it was as if the killer was trying to turn his victims inside out. This ritual bore an eerie resemblance to the literary accounts of how one could be “turned over” like a glove by moving around a plane that cut through the body from navel to spine, in order to rotate through the fourth dimension and into one’s mirror image.
It is perhaps a coincidence that the first modern serial killer seemed to mimic the fantasies of anatomical reversal that emerged alongside the modern conception of (n-dimensional) space. It has nonetheless been speculated that Lewis Carroll could have been Jack the Ripper—the cut-out face of the Ripper’s last victim, Mary Jane Kelly, resembled the faceless smile of the Cheshire Cat.26 Other suspects with conspicuous connections to the fourth dimension are not in short supply: for example, the royal physician Sir William Gull, whose close friend James Hinton was the father of Charles Howard Hinton. Hinton himself, a convicted bigamist, would have made for a prime suspect, had he not been in Japan at the time of the murders.


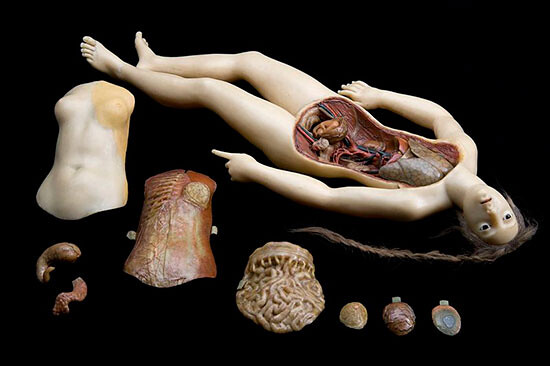
But there were other things that could constitute a threat to the sanity of the Victorian gentleman, in addition to staring at colored cubes piercing a three-dimensional plane. Anatomical models that idealized and sexualized female corpses—the so-called anatomical Venus—were a common staple of medical schools. The yearning for an unresisting and unrejecting object fueled fantasies of an infantilized Womanhood––like the photographs of Alice Liddell, the child Alice of Carroll’s books—and gave rise to a fascination with unresponsive bodies. Since procuring children was more socially acceptable than procuring corpses, pedophilia fostered a booming brothel industry, whilst necrophilia sought refuge in literature and the visual arts.
Is the fourth dimension a mathematical hypothesis or a sexual phantasm? Partial objects, as Lacan put it, are not biologically given but an effect of the signifying system of language. The fourth dimension was at once a mathematical construct and a fear of mutilation, which went hand in hand with a longing for “complete” genitalia as the place of erotic fulfillment. As Simone de Beauvoir would later argue, one is not born a woman (or a man)—one becomes one. What appears as gender is indeed an effect of the way space is partitioned, but as Poincaré pointed out in the year prior to the Ripper’s murders, the word “space” can refer to different things: physiological space, which is defined by motor, tactile, and visual perception; and geometrical space, which is infinite and homogenous.27 There is a third category that Poincaré left out, however. The word “space” can also refer to social space, that elusive entity whose vectors warp morphology and chronology, and cut through the mathematical, the psychological, and the political—and whose nature remains hard to fathom, but whose weight is always somehow borne by women’s bodies.
See Martin Gardner, “The Fourth Dimension,” in The Philosophy of Left and Right: Incongruent Counterparts and the Nature of Space, eds. James Van Cleve and Robert E. Frederick (New York: Springer, 1991), 61.
Quoted in Alexander Koyré, From the Closed World to the Infinite Universe (Baltimore: John Hopkins University Press, 1957), 245.
In later writings Kant came to espouse a different view, namely the one we usually identify with Kantian Idealism. The Kantian synthesis entailed a reconceptualization of the dichotomy between absolute and relational space over which Newton and Leibniz had contended, into the opposition real vs. ideal. Space, Kant argued, is absolute and independent from material bodies because it lacks concrete reality: space is a form of human perception, it is our subjective means of cognizing the world. Thus it is ideal (or mental) rather than real.
Gardner, “The Fourth Dimension,” 63.
The dimension of a mathematical space is usually defined by the minimum number of coordinates necessary to specify a location in it: a cube, for instance, has dimension three, whereas a hypercube—the four-dimensional analogue of the cube—has dimension four. In ordinary language one is nevertheless tempted to say that a hypercube has four dimensions, which implies corporeality.
Hermann von Helmholtz, “On the Origin and Significance of the Axioms of Geometry,” Mind, Vol. 1, No. 3 (July 1876): 301–321.
The claim was made in the “Queries” appended to Newton’s Opticks. He later allegedly attempted to recall the whole edition.
Courtenay Grean Raia, “From ether theory to ether theology: Oliver Lodge and the physics of immortality,” Journal of the History of the Behavioral Sciences, Vol. 43, No. 1 (Winter 2007): 18–43.
Bruce J. Hunt, “Lines of Force, Swirls of Ether,” in From Energy to Information: Representation in Science and Technology, Art, and Literature, eds. Bruce Clarke and Linda Dalrymple Henderson (Stanford: Stanford University Press, 2002), 100.
Other observers included William Edward Weber, professor of physics; W. Scheibner, professor of mathematics; and the above-mentioned Gustave Theodore Fechner, professor of physics.
The Seybert Commission (1884–87) was an investigative committee created by the faculty of the University of Pennsylvania to scrutinize the claims of spiritists and mediums.
Linda Dalrymple Henderson, The Fourth Dimension and Non-Euclidian Geometry in Modern Art (Princeton: Princeton University Press, 1983), 28.
Stringham’s article was published in the American Journal of Mathematics.
It was Hinton who introduced the term “tesseract” for what is regularly known as the hypercube. The word combines the prefix τέσσᾰρᾰ, meaning “four,” and the word ἀκτίς, meaning “ray” (after which the radioactive element actinium was named). Each vertex of the tesseract would cast out a ray, able to pierce through interdimensional space.
Bernhard Riemann had also anticipated that gravity and electromagnetism were the effects of spatial distortions. Einstein would later add that the gravitational force is not a force per se, but a property of four-dimensional space-time.
For Kaluza, light can be explained as a vibration in the fifth dimension (after Einstein, the fourth would be described as time.) What became known as Kaluza-Klein theory is fundamental for string theory, which describes the properties of matter as gravitational vibrations (or strings).
Letter from Hiram Barton to Martin Gardner about Gardner’s review of Hinton’s work. The letter is reproduced in full here →
In Carroll’s world, where there are no absolute “Laws of Nature,” all sense of proportion (both literal and metaphorical) is lost and Alice finds it hard to keep her size constant. She also meets a caterpillar who is sitting on a mushroom while smoking a hookah, a phallic overkill which hints at the sexually charged imagery of everything oriental for Victorian audiences (algebra is derived from the Arab al jabr).
Carl B. Boyer, A History of Mathematics (Hoboken, NJ: Wiley, 1968), 18.
This slippage between the language of algebra and the language of geometry will create a belief in the reality of transcendental space. In the “Lion and the Unicorn” episode in Alice in Wonderland, Alice says she sees “nobody” coming down the road, to which the King replies, “I only wish I had such eyes … to be able to see nobody! And at that distance, too”—thus hypostatizing “nobody” into a proper noun. See Elizabeth Throesch, “Nonsense in the Fourth Dimension of Literature,” in Alice Beyond Wonderland, ed. Cristopher Hollingsworth (Iowa City: University of Iowa Press, 2009).
Bertrand Russell, Foundations of Logic, 1903–05 edition, eds. Alasdair Urquhart and Albert C. Lewis (London: Routledge, 1994), 579.
Henderson, The Fourth Dimension, 32.
Jean Clair, Sur Marcel Duchamp et la Fin de l’Art (Paris: Gallimard, 2000), 167.
See Susan C. Lawrence and Kae Bendixen, “His and Hers: Male and Female Anatomy in Anatomy Texts for U.S. Medical Students, 1890–1989,” Social Science & Medicine, Vol. 35, No. 7 (1992): 925–934 →
Ibid.
See Richard Wallace, Jack the Ripper: Light-Hearted Friend (Melrose, MA: Gemini Press, 1996).
Quoted in Henderson, The Fourth Dimension, 36.