Truth Is in the Tower

Part I: The Spatial Architectures of Computational Truth

The Arab-Islamic Renaissance, which unfolded from 800 to 1200, remains a lacuna for Western historiography. The family of technological innovations dating from the period includes the camera obscura, the first automata, and the work of al-Khwarizmi, namesake of the “algorithm”—a diaspora of premature anachronisms which effectively disrupt our narratives of technology’s advance in the West’s own Renaissance.1 The work of logician Ramon Llull, born at the edge of this diaspora, in Mallorca in 1232, is a kind of aftershock occurring at the temporal and spatial periphery of these seismic technological transformations that this “first” Renaissance produced. Serially forgotten and retrieved throughout history by figures as disparate as Alberti, Leibniz, Descartes, Eco, and Calvino, Llull’s work is both a distant echo of an event already deleted, and the enduring pathological legacy of our historiographic blind spots.2

Detail of Aristotle, Breviculum. Badische Landesbibliothek, code: St. Peter perg. 92. Kalrlsruhe.

In 1321, six years after Llull’s death, his student, Thomas Le Myésier, in a bid to secure his master’s legacy and his own no doubt augmented role in the production of this legacy, gathered Llull’s masterwork Ars Genralis Ultima, and its abbreviated version, the Ars Brevis, in a volume named the Breviculum. In order to illuminate this work, he commissioned twelve miniatures depicting “The Life of Ramon Llull.” Miniatures VI and VII depict truth abducted and being held prisoner in the tower of falsehood, from whose battlements and windows hang the monstrous demons of untruth. To the left we see wickedness, inactivity, ignorance, weakness, confusion, disaster or falling, futility, and nothingness; and, to the right, depravity (or distortion—the medieval sense of this one is not totally clear), impossibility, hatred, falsity, punishment, contrariness, emptiness, inflexibility, abundance in the sense of excess, and diminution.3 This sinister tower is a play on the towers of truth, which ascend to the heavens, and those various other memory devices, the mnemonic towers of facts whose performance, along with that of mnemonic trees, hands, ladders, and arks, was central to medieval synthetic thought.4

Looking at this miniature, we can’t see truth, but we can hear her calling out to be freed: a lamentation appears at the lower left of the page:

“Have mercy, have mercy on me, at least you, my friends! The hand of ignorance touched me, and in my place faithless opinion was crowned in public. I, in contrast, who dreads every dark corner, am buried entirely against my will in darkness and without light in the depths of the dungeon. Sad, deserted, and almost desperate I die! There is no one to help me or give me comfort. On the contrary: many are more inclined to support false opinion than to free me from the dungeon. All you philosophers, in whom—apart from God—I place my entire trust, since you are the true lovers of wisdom and truth, please come to my aid, I beg you; otherwise I must perish by inaction!”5

The philosophers have heard. Riding to her rescue are three parties in chariots which it turns out are also towers—mobile siege towers. Within Le Myésier’s staging, the fate of truth is suspended between the fixed tower that holds her captive and the three mobile towers that would liberate her.

At the front rides Aristotle on his horse Ratiocinatio, “rational reasoning,”6 armed with the syllogistic apparatus of Greek logic. In his chariot are the five general propositions of logic, but also the peculiar and the accidental, yet to be excluded from his formal system. Although it is the beginning of the end for them: they won’t be tolerated for too much longer.

Detail of Averroes’s Beviculum, Badische Landesbibliothek, Code: St. Peter perg. 92. Kalrlsruhe.

Behind Aristotle rides Abu al-Walid Muhammad ibn Ahmad ibn Rushd—known to the Latin West as his commentator, Averroes—on his horse Imaginatio, and armed with imagination. Averroes maintained the existence of a twofold truth in which a proposition may be philosophically true but theologically false. Despite the inclusion of Averroes here, Le Myésier’s disapproval of this position is clear from the text below the image, which states that Averroes “did not know the truth, or had not concerned himself with it, because he disapproved of it just as much as he could.” Worse still:

He denied eternal life, and argues that the greatest joy lay in observation, which is perfected in the speculative sciences. He did not turn to the inner activity of God, just as he did not attend to his creative outward activity, unconcerned that every activity is directed to the goal and to perfection. Neither did he care to recognize the nature of the divine dignities or their activities: nor their unity in the individual differentiation of activity, without which God would forever remain inactive in himself and without any majesty. Consequently, he would in his entire nature be imperfect and ultimately unworthy to be God.

Heretic Averroes, ostensibly unmotivated by perfection-seeking abstract thought, argued that we are only capable of thought in union with our body. Given that Llull, as we shall soon see, would eventually dispense with the body altogether, we can only assume Le Myésier tolerates the presence of Averroes in this miniature tripartite philosophical alliance for strictly strategic and temporary reasons.

Ramon Llull. Breviculum, detail. Badische Landesbibliothek, code: St. Peter perg. 92. Kalrlsruhe.

And at the rear is Ramon Llull on his horse Recta Intentio (“right intention”), and armed with his Ars. If first-degree knowledge was understood as sensible knowledge from sensible things, then Aristotle, with his tolerance of the accidental, and Averroes, with his pursuit of happiness from observation, are in the business of producing second-degree knowledge, intellectual knowledge of sensible things, in which perception provides input data before abstract reasoning takes over. But the axiomatic system of Llull’s Logica Nova takes this decorporealization a step further by excluding perception entirely, thus producing third-degree knowledge: intellectual knowledge of intellectual things—precisely the kind of inward-turning thought Averroes is apparently incapable of.

The script on Llull’s lance makes the abstracted nature of his newly hermetic system of logic for a vita contemplativa abundantly clear: “He who wants to know the spiritual must transcend senses and imagination, and often himself.” This is the beginning of the production of truth cut off from the senses and thus insulated from the corruptions of our bodies and their creaturely limitations. This decorporealization of truth is truth getting ready to be housed in another kind of body, the machine of thought that is still as yet to be imagined. But already there is a sense that mechanized thought, being uncontaminated by the error that plagues human cogitation, will necessarily think no falsehoods.

Llull’s passengers. Breviculum, detail. Badische Landesbibliothek, code: St. Peter perg. 92. Kalrlsruhe.

Riding alongside Llull in his chariot are the nine absolute principles or concepts of his Ars Magna: goodness, greatness, duration, power, wisdom, will, virtue, truth, and glory—all pseudonyms for God, we should note—though only greatness looks like he is having a good time. Behind them are the nine relative principles or predicates: concordance, difference, contrariety, beginning, middle, end, majority, equality, and minority.

Llull’s engine. Breviculum, detail. Badische Landesbibliothek, code: St. Peter perg. 92. Kalrlsruhe.

Note that unlike those of Averroes and Aristotle, Llull’s chariot has a souped-up engine, the fire column, fueling his triadic reasoning systems—be it his Ars Demonstrativa, Generalis Ultima, or Brevis (each the software update of the previous). This fire is telling us that reason’s machinic home, when it finally arrives, will be prodigiously powered.

“Figure A” or “Absolute principles.” Ars Brevis, late fourteenth century, Colecciones Reales, Patrimonio Nacional, Biblioteca del Real Monasterio de San Lorenzo de El Escorial. Diagram by Zsuzsa Peters, 2016.

Within his Ars Magna, we meet Llull’s absolute passengers again, as the nine letters, B–K (no J), in his Figure A.7 The connecting lines in Llull’s diagram assert from the outset the potential of mutual transposition within this system: God is great, great is good, etc. They also assert the essentially active or performative nature of the terms, all of which are lent activity: it is not sufficient for something to simply be good, it must also do good or produce good in order to satisfy Llull’s conditions. His system is relational from the start, by virtue of its triangulation between terms, thus anticipating Leibniz’s belief that relations, not substances, come first—not the other way around, as Isaac Newton would have it.

This triangulation, with its cybernetic ambitions, is also the footprint of the trinity. The raison d’être of this system is the conversion of Muslims and Jews to Christianity, via logic only. There is no mention of any Christian-specific term in the whole system, but it is hardwired in with a triadic system—father, son, and holy ghost. Christianity’s only signature here is spatial. This machine of thought “was planned as a kind of deductive apostle of the faith,” as Ernst Bloch described it. Llull’s goal was to convince all unbelievers of the truth of the Christian religion by means of the irrefutable and, crucially, transparent demonstrations of his machine which, being mechanized, was already, automatically, “free of every error in reasoning.”8

“Second Figure/Figure T” or “Relative principles.” Ars Brevis, late fourteenth century, Colecciones Reales, Patrimonio Nacional, Biblioteca del Real Monasterio de San Lorenzo de El Escorial. Diagram by Zsuzsa Peters, 2016.

Llull’s Figure T is divided into nine chambers, or cameras, which house the nine relative principles. A substructure of lines sets up loyalties between three predicates, creating the three trinities: concordance-difference-contrariety, beginning-middle-end, and majority-equality-minority.9

Within Llull’s Table, our passengers and their letters take on different meanings depending on which figure they find themselves in, e.g.: B in Figure A means “goodness,” while in T it means difference, while in Questions and Rules it means “whether,” and in Vices it means “avarice.”

“Third Figure” or adjacency matrix of absolute and relative combinations. Ars Brevis, late fourteenth century, Colecciones Reales, Colecciones Reales, Patrimonio Nacional, Biblioteca del Real Monasterio de San Lorenzo de El Escorial. Diagram by Zsuzsa Peters, 2016.

Figures A and T are combined in Llull’s Third Figure, in which each pairing—given that each letter represents a different meaning in A or T—can generate twelve clauses. These pairings are commutable, so only half of Llull’s adjacency matrix is ever present.10

“Fourth Figure.” Ars Brevis, late fourteenth century. Colecciones Reales, Patrimonio Nacional, Biblioteca del Real Monasterio de San Lorenzo de El Escorial. Diagram by Zsuzsa Peters, 2016.

Llull’s final iteration of his ternary combinatorial system culminates in the Fourth Figure, which introduces three concentric wheels able to generate tertiary combinations between the principles and relative principles, thus establishing what Donald Knuth calls Llull’s “three-valued logic”: true, unknown, false.11 Thus the presence of the trinity not only unwittingly installed a dynamic relational architecture, it also installed a possibility of indecision that later binary architectures would deny.

Is the world eternal?  Zsuzsa Peters, 2016.

By combining all of the above (along with Llull’s Definitions and Rules, which we will come to), we have a system of which we may ask any question and calculate an answer—such as, is the world eternal? This question is posed in terms of BCD, whereby B is “whether” from Questions and Rules, and C and D from Figure A are “greatness” and “eternity,” respectively, on the basis that for anything to be eternal it must also be great. The algorithm generates the answer: no.12

Like all the formal logic and universal language systems that followed, Llull’s Ars is highly reductive and compressive in its makeup, comprising a set of basic truths designed so that any process can be broken down into a series of fundamental operational steps. This mandated processing of only-one-thing-at-a-time has constrained every computer since, no matter how powerful. The spatial reduction it delivers is not simply a response to archival exigencies but also key to reactivating knowledge.13 Such systems are always hermetic: the system must be closed so that it can be exhaustive in its iterative testing of combinatorial possibilities in the production of different meanings. Thus, by redefining truth as a limited set of undeniable elemental truths pertaining to all fields of knowledge, hermetic systems claim to be able to calculate all possible truths. This is recursivity in service of universal truth production, in which the initial reductive action is always taken with a view to ultimate expansion. Don’t be fooled by the spatial modesty of compression! Its ambitions are always colonial. Kircher neatly formulated this double strategy of compression-plus-expansion some three hundred years later, in his 1663 proposal for a universal language, the Polygraphia Nova et Universalis, which promised: The Reduction of All Languages to One—The Expansion of One Language to All. It is curious to note that beyond these first and second promises, the third promise this system made was that of encryption via “A Techno-logia; or, a universal Steganographic Secret operating by combinations of things; whereby, through a technique impenetrable to the human mind, one may transmit one’s secrets to another in nearly a thousand ways.” This took the form of a box (a physical three-dimensional matrix labeled “A Glottotactic Ark good for writing letters throughout the whole world”) and a user’s manual. All promises, though undelivered by their maker, have now come to pass in the form of the ultimate compressive/expansive language of zeros and ones. Returning to Llull, his Rules further equip us with nine epistemological tools in the form of nine interrogatory modes:

Kliment Voroshilov, Vyacheslav Molotov, Stalin, and Nikolai Yezhov on the shore of the Moscow-Volga canal. After Yezhov was tried and executed, he was removed from the photo. © Courtesy the David King Collection.

Utrum—whether. (This is the freest of the rules, problematizing mere possibility. It has three subspecies—affirmative, dubitative, and negatory—“so that,” as Llull writes, “the intellect is not obstinately bound to an opinion.”)

Quid—quiddity. What is it from?

The White House posted President Obama’s long-form birth certificate on April 27, 2011. See →.

Quare—formal cause. Why?

[top] The Vote Leave battle bus. Jack Taylor/Getty.[bottom] Greenpeace rebrands the Brexit bus. Greenpeace, UK.

Quantum—quantity. How much?

Crowds attending the inauguration ceremonies of President Donald Trump (L) on January 20, 2017, and President Barack Obama (R) on January 20, 2009, in Washington, DC. Reuters/Lucas Jackson (L) and Stelios Varias (R) tpx images of the day.

Quale—quality. Which, of what kind?

“Fake Rice Being Made In A Factory In Vietnam – Fake Plastic Rice Warning,” YouTube video watched by almost two million people in a year →.

 

Quando. When?

Digital effects used in Rogue One: A Star Wars Story to resurrect Peter Cushing as the character Grand Moff Tarkin. Industrial Light & Magic/Lucasfilm.

Ubi. Where?

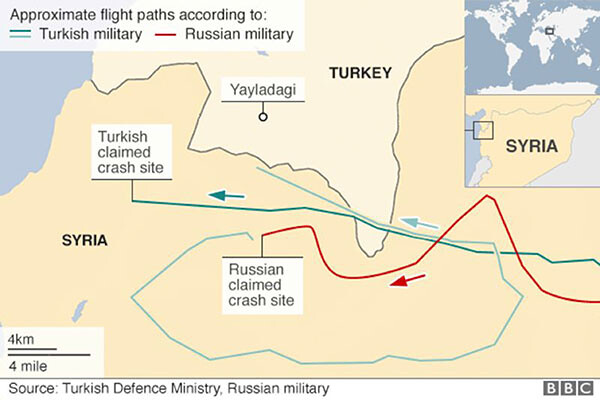
Purported flight paths of Russian SU-24 shot down by Turkish military on November 24, 2015. Compiled by BBC →. 

 

Quo modo—modality. How?

Ivanka Trump replaces President Donald Trump at the third working session of the G20 meeting, July 8, 2017, Hamburg, Germany. Photo: Ludovic Marin/AFP/Getty Images.

Cum quo—instrumentality. With what or whom?

Plato’s Allegory of the Cave in the century of Pepe the Frog.

All of which are still busy on the frontlines of the current information wars.

Llull serially refined throughout his life the relations between the principles, predicates, and the Questions and Rules in search of their clearest, most efficient, but also most seductive presentation—their best user interface. Early formulations (the Ars Compendiosa Inveniendi Vertitatem and Ars Demonstrativa, both of 1238) were modified during what is known as the Ternary Period in Llull’s production, by the introduction of the trinity with the Ars Generalis Ultima in 1305 to better appeal to Christian readers, and then abbreviated for easier consumption and thus better uptake in the form of the Ars Brevis in 1308. This Ars of conversions was, like all such universal systems, first and foremost an Ars of conversion to itself. Via Llull’s wheels, the derivation of proofs could be demonstrated ad oculus, within this newly transparent logical artifice. Once converted to the apparent transparency of such an interface, the system behind it might lead the user anywhere its designer so desired.

Ars Inveniendi Particularia in Universalibus (ms.IV-6, fol.16), Colecciones Reales, Patrimonio Nacional, Biblioteca del Real Monasterio de San Lorenzo de El Escorial.

If this sounds more familiar than medieval, it is curious to note that Bloch places Llull, with his aspiring machine that might satisfy what he describes as “bourgeois calculation needs,” in the four-hundred-year-old project of European modernity.14 Although quite how is unclear—Llull was fashionably early by some three hundred years. Bloch, in exile in 1930s America, described Llull’s Ars Demonstrativa as a “logical logarithmic clock,” a kind of “deduction machine of knowledge [that] should encompass and exhaust every variation of cognition that was at all meaningfully possible.”15 He simply might have said, as others have since, that it was for all intents and purposes the first computer. While Llull’s paper machine used (fuzzy) words, it did so in a combinatorial and thus “discrete” or absolute way, as if they had sharp edges and could be treated as discontinuous terms, numbers on the clock face at the back of Bloch’s mind, even though they clearly still exerted a symbolic pull, a tugging web of metaphoric linkages to their natural-language counterparts. If Friedrich Kittler called Turing’s machine the universal discrete machine, or “the manic-cutter,” we might call Llull’s Ars the universal, very nearly discrete machine, whose cuts were never quite clean.16 Despite their messy cuts, the loyalty of the words and letters in Llull’s Ars to algorithms rather than to natural languages marks a turning point in Kittler’s “2,000-year-old war between algorithms and alphabets and between numbers and letters”17 and their delivery of the truth: truth that is better because it is mechanized and thus makes no errors. Should the user be in any doubt, the Ars’s multiplicitous structure allows twenty routes, and thus twenty proofs, to the answer of any question.

Cod. Cus. 83: Raymundi Lulli Opera, 1428. St Nikolaus Hospital-Cusansstif-Bibliothek, Bernkastel-Kues.

How are we to read to these paper circles and the nascent machine their hybridity augurs? As drawings or as wheels? As representation or as mechanism? Aristotle describes thinking, the production of knowledge, and thus, hopefully, of truth, as activity. Llull’s third-degree knowledge—intellectual knowledge of intellectual things—completed the decorporealization that Aristotle started, disembodying thought. But, being active, thought must still somehow move between its three constituent nodes, which Llull describes as the knower, the known, and the act of knowing (or more beguilingly, the lover, the beloved, and love itself). Such decorporealized thought must be lent some other body that moves, but a body-without-senses this time, a senseless body: the machine. The rehousing of thought in the machine results from Llull’s decoupling of thought from Aristotle’s senses—and not vice versa—in which thought that is hermetically sealed within the intellect (of the intellect, by the intellect, with the intellect) must, like a lion in its cage, turn in circles in order to satisfy its need to move.

Detail, Breviculum. Badische Landesbibliothek, code: St. Peter perg. 92. Kalrlsruhe.

But these paper wheels also facilitate other movement, other cycles. At the end of Ars Demonstrativa, Llull solves each of the 1080 questions by means of chains of compartments containing letters or terms drawn from the figures—a flowchart that incorporates the conjunction “and” and the disjunction “or.” In their deductive action, the axiomatic cycles and subcycles describe an algorithmic structure of recursive logical operations that are, in turn, able to generate algorithmic artifacts. In this turning machine then, truth is secured as an algorithmic product. The autopoietic constitution of the Ars also means that truth, an algorithmic artifact, is able to produce other algorithms—is able to ask itself and answer new questions.18 Peter Weibel argues that Llull’s algorithm of concepts remained unchanged until 1879, with the publication of Gottlob Frege’s Begriffsschrift: eine der arithmetischen nachgebildete Formelsprache des reinen Denkens (Concept-Script: A formal language modeled on that of arithmetic for pure thought), whose strange logical syntax influenced Ludwig Wittgenstein in his own project to eliminate falsehoods.19 The verb “to err”—to drift from a true course—reminds us that the architecture of any algorithm (always an essentially corrective system, even when it is not in delivery of religious conversion) is primarily circulatory, a set of corridors and decision-gates through which data is irrigated without fear of deviation. Just as the immaterial architecture of archery and projectiles produced the geometry of the counter-architecture of the Renaissance fort, this tower of falsehood, with its distortion, inactivity, and confusion (to name but a few inhabitants), produced the counter-architecture of the algorithm, whose irrigating corridors might defend us from those same multicolored beasts.

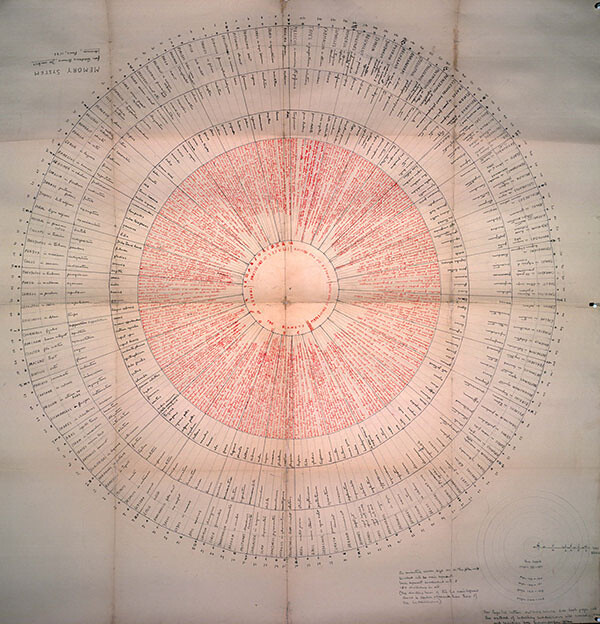
Frances Yates’s reconstruction of Giordano Bruno‘s memory wheel from De Umbris Idearum, Paris, 1582. Warburgh Archive, London.

Returning to our rescue party: If we imagine the line of philosophers continuing behind Llull, who else is there? Giordano Bruno, who loads the wheel with so much memory storage that it stops revolving but is lent other dynamics, with its esoteric data compression and decompression functions and tortuous storage and retrieval pathways. Kircher, whose Arca Steganographica, with its enmeshing of cryptography and computation, became the formal/causal precedent for the Enigma and the Colossus.

“Universal Languages” as presented by Cave Beck (1657), John Wilkins (1668), and the US Department of Defense (1960).

Hot on their heels are certainly Francis Bacon and John Wilkins, whose distrust of natural languages and the slippery promiscuity of words, which always lead thought astray, motivated their proposal for a universal language of real characters (still letters) that would eradicate all errors. Flanking them is Cave Beck, who, going the full mile, dumped letters and expressed all terms in numerical values, using 0–9.20 Then there is Leibniz, in whose De Arte Combinatoria the ratiocinator and the binary never quite combined.

Nor did they in the work of the still unsung Ada Lovelace, nor in the brass baggage of Charles Babbage, with his industrialized arithmetic, until Turing, with George Boole and Kurt Gödel in the wings, merges Leibniz’s binary with conceptual operations, writing all concepts, logical operations, and their interrelations in zeros and ones. Thus, as logical operations become mathematical operations, thought, or the production of truth, finally becomes calculation—all of this predicated on the if-then of Aristotle’s first syllogism.

In 1986, in a strange inverse archaeology, Werner Künzel and Heiko Cornelius converted Llull’s Ars Magna into COBOL (a contemporary programming language) and then into an Assembler application, which was inputted into a computer. Llull’s triadic thinking entered the operational space of the then contemporary digital algorithm, whose recursive footprint it would have recognized. It would even have recognized the potential promiscuity of the system’s application, as the Ars was intended to recombine not only Averroes’s segregation logic and theology, but also rhetoric, literature, and metaphysics in a medieval multidisciplinary space where new syllogisms, and fallacies, might be added to classical ones—though it may well have wondered why these fields were now nowhere to be seen within its interrogations. Kurt Gödel, in 1931, in famously showing that mathematics produces propositions that are not decidable, not provable, and therefore indecipherable by a machine, effectively revealed an invisible architecture of ever shrinking horizons. The domain of truth is redrawn as the smaller subdomain of provability, and that of provability as the even smaller subdomain of that which is provable by binary computation. The opera aperta, as Umberto Eco was to describe Llull’s Ars, had somehow become much less aperta, though it still, to quote René Descartes on the Ars again, “allows one to speak on many subjects without knowing any of them.”21

But it is not just the uncomputable or undecidable that must be excluded, that must remain imprisoned outside the algorithm’s infinite corridors. To the left of the tower is written the task for the philosophers: “By destruction or distinction, destroy the tower.” This distinction of difference was to become so distinct in the (difference) engines to come, that all analogue continuum was ruled out, in pursuit of discrete truth, despite the fact that it abbreviated complex relations by rewriting transitioning curves as dumb, discrete steps. Illicit curves did survive in the minor history of analogue computers: as late as 1979, Soviet analogue water computers—descendants of Vladimir Lukyanov’s 1936 Gidrointegrator, a kind of calculation by plumbing—were still outstripping their digital counterparts in exactitude, unhampered as they were by the requirement to approximate relations between values. If we let our eyes wander down our imaginary, extruded line of rescuing-philosophers listed above, we see with each, as their falsehood-eradication systems became more discrete in what they included and excluded, more universal in their application and their suppression of alternatives, more heavily fortified against dissent, more effective in their colonization and monopoly of the production of truth, the more extraordinary the errors they produced. Accuracy per se was no longer the goal, as exactitude gave way to truth defined by speed and, above all, its ability to dominate.

Llull’s three heralds. Breviculum, detail. Badische Landesbibliothek, code: St. Peter perg. 92. Kalrlsruhe.

Llull’s machine approximated (and corrected) thought. Universal languages approximated (and corrected) their natural counterparts. Discrete values approximated any continuum as numerical values approximated (and corrected) Enlightenment real characters. And the binary approximated the indeterminacy implicitly tolerated by Llull’s ternary. Returning to this miniature, we are reminded that Llull’s chariot, unlike the others, is preceded by heralds bearing trumpets, three to be exact—the three reasoning angels that still comprise any machine of thought: reason, will, and memory. In his writings, Llull grants us humans a sixth sense: that of communication—cybernetics’ twin to control. Even outside of his cross-referencing Figures, Llull rarely if ever presents any foundational aspect in an isolated manner but instead in a complicated web of relations between different components. Amadore Vega argues that Llull was “foretelling an order of connections that was much richer and more complex than the merely vertical (Platonic) or horizontal (Aristotelian).”22

Llull’s three trumpets. Breviculum, detail. Badische Landesbibliothek, code: St. Peter perg. 92. Kalrlsruhe.

From the angels’ trumpets pour lines of words that converge and bifurcate as they exhaust their mutual permutational set of the trinity: God, the Creator, and the Savior. The weapon of truth Llull carries, powered by that burning engine in the back, having relational ambitions, reads the world in terms of threes. (Not at base three—Llull would count like us to base ten, but in terms of a triadic structure.) Thus, in Figure T, the relational figure, we saw: beginning, end, and middle; concordance, contrariety, and difference; majority, minority, and equality. This paradigm is constitutionally different from the binary paradigm of Kittler’s “manic-cutter,” which he describes as the inevitable product of the always binary zero-sum game of war—you win or you loose. No halfway house. But Llull’s triadic system crucially did allow this possibility, this halfway house. Moreover, this triangulation of relatedness, which necessarily arose from his use of the trinity, allows feedback, and thus cybernetic action (remember the known, the knower, and the act of knowing). In so doing, Llull’s trinity-induced performativity anticipated everything that in the twentieth century finally undid causal linearity and gave way to the looping recursivity of cybernetics and the new machines of life.

But there is yet more which leads us from the algorithm’s corridors to our third and last architectural figure, the screen. Aristotle’s syllogism, if A and B then C, uses two variables, is quadratic—i.e., two dimensional—and can be spatialized with an x-y matrix. Today’s computers, being binary and thus “genetically” constrained by Turning’s machine, are still quadratic. Although they may admit a long list of variables—if A and B and C and D or E and F then Z—in reality their processing can only deal with one pair at a time, the final pairs being paired up. Llull’s triadic system, however, in adding a third variable, created a cubic system—if A and B and C then D—that is crucially processed in triplets.

Tabula Generalis and Second Figure. De Auditu Kabbalistico, sixteenth century, Fundación Bartolomé March-Biblioteca, Palma de Mallorca.

But how was Llull to represent this? The adjacency matrices and graphs that had displayed his earlier quadratic systems were unable to accommodate such cubic ambitions. At first Llull produced a kind of bastardized x-y matrix, the Tabular Generalis, in which what were effectively values for the z axis were distinguished by inserting a syntactical separator denoted by the letter T. This acted as a wall, establishing a separate chamber or camera for z values to the right or left of it—a letter on the left of this wall was to be read as a y variable while the same letter on the right of this wall was to be read as a z variable. But this was clearly unsatisfactory. And so, unable to draw a three-dimensional matrix to house his cubic system, Llull drew a wheel.23 His vouvelles, as they were called, brought with them many attributes that a three-dimensional adjacency matrix, could he have drawn it, would not have: they allowed multiple interpretations to be simultaneously tolerated, with the dominant truth at twelve o’clock and additional truths around the clock face. Further, by virtue of geometry, they allowed the possibility of additional wheels, potentially an infinite set—this system could grow and grow in its complexity.24 But in solving Llull’s representational dilemma, the wheel did something else that a three-dimensional matrix might have prevented: it let form in, and in particular, surface. And then surface did its thing as it squashed the cubic space of the ternary into the flat space of the wheel. The heirs of Llull’s wheels forgot the invisible cubic space of their operation that the trinity had procured, and remembered only what they saw: the flattening of all operations at the surface—the interface. The problem of knowledge has always been the problem of its representation. This was truly a triumph of representation.25

Thus the presence of the wheel in this first machine of thought is not simply about the need for thought to move, and for this moving line to also somehow stay put and not run over the horizon. It is also about a crucial flattening of space. Digital space was born flat. And, tellingly, this happened at the interface: where we can see it—all at once, all the time. The flattened space of Llull’s representational vehicle took hold and somehow endured in its prefiguration of the flat space of the screens to come. As if our demon-infested tower has been unwrapped, unfurled, and is now presenting its flattened internal façade to the world, concealing behind the siege of truth calculating algorithms whose multiplying action delivers us an infinitely multiplicitous surface.

In 1671 Leibniz takes Llull’s wheel (with its still fuzzy figures), and in his ratiocinator lends it cogs—the almost discrete was now indisputably discrete, and digital, base ten.26 At the same time he resurrects the ancient Indian binary.27 Words are gone, as is any triadic structure—and lost with it are the relational web and the middle undecided option. This is because, as Leibniz famously wrote to Mersenne, “once we have realized this language, calculating and reasoning will be the same thing.”28 Thus, discreteness (an inherently gross approximation of any continuum) secured the way for the engineered neutrality that the Ars had already paved; in order to bring about the conversion of Jews or Muslims through reason only, the Ars had needed to appear theologically neutral and nondoctrinal. Llull declares this strategic indifference as the property that distinguishes his Ars from both metaphysics and logic: “Metaphysics considers things exterior to the mind insofar as they concern their reason for being; logic, however, considers things according to their existence in the mind; but this Art, as the highest of all human sciences, considers being indifferently according to one mode or another.”29 Thus the construction of neutrality that is now the aboriginal hallmark of the machine of thought, like the decoupling of thought from the senses, was also formulated ex machina, before being installed in the machine, its newly adopted site of origination and, ever since, the site of mechanical objectivity: Thomas Nagel’s view from nowhere. The engineered neutrality of the machine of thought has played the role of arbitrator in every domain of “truth” production. We saw the strange abdication of authorship that this produced in the discourses surrounding parametric design in architecture, and now this same engineered neutrality, with the advent of machine learning, authors not simply the parking of our cars but also the selection of our lovers, the bail decision in our law courts, and the tailoring of our very own personalized newsfeeds.

Turkish president Recep Tayyip Erdoğan speaks to CNN Turk via FaceTime during the attempted military coup of July 15, 2016. CNN online.

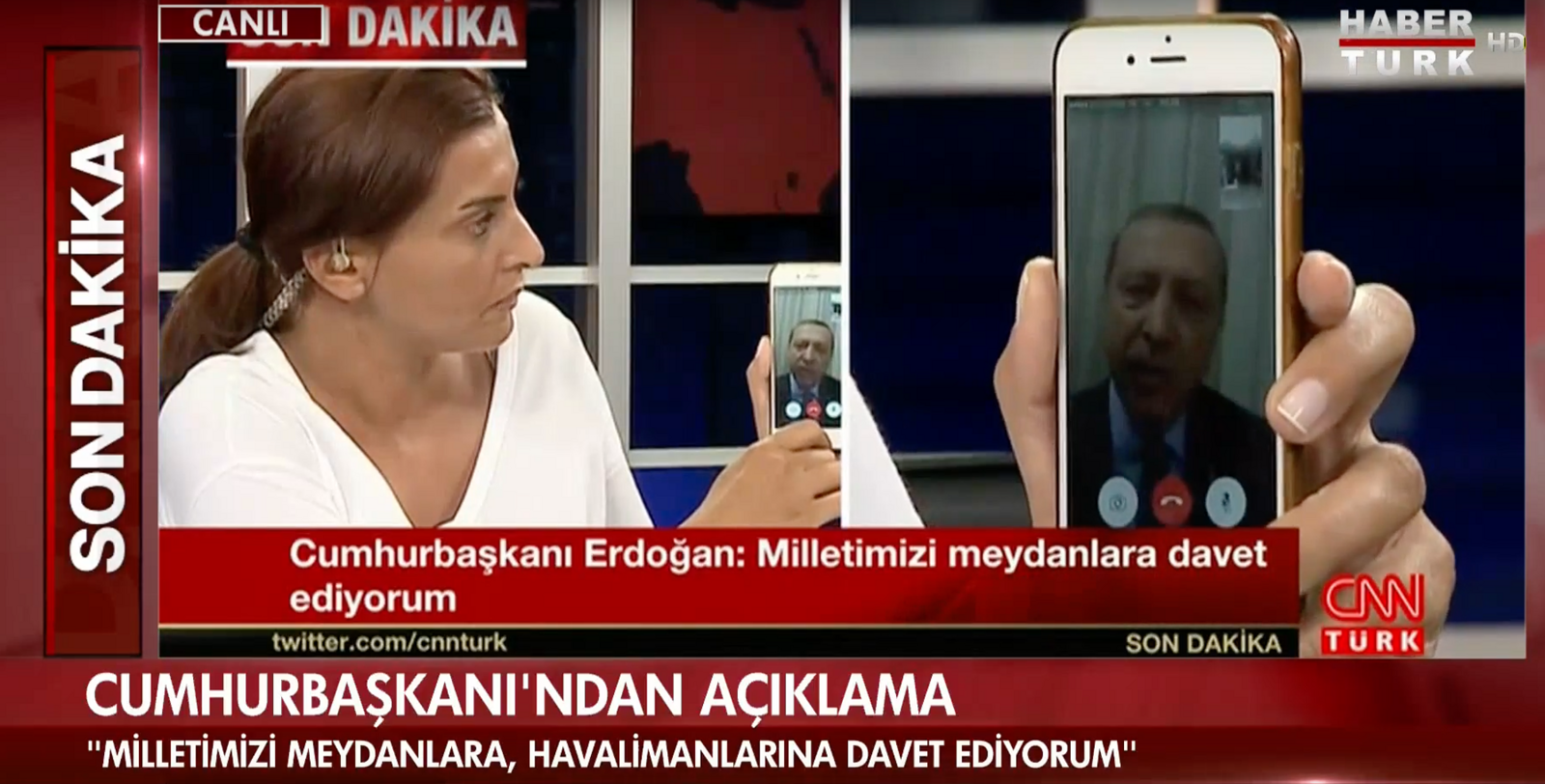
Today, the panoply of screens that make up our immersive and, often, tailored tele-scape is our tower—the latest architecture in which facts are still serially constructed and reconstructed in an eternal present, as their “truthiness” profiles rise and fall and rise again. This multiplicitous mise en abyme of zero depth (think of Recep Erdoğan’s phone talking to a screen during a coup) is again truth without the z axis: flat truth.

The demons of untruth. Left: wickedness, inactivity, ignorance, weakness, confusion, disaster or falling, futility, nothingness. Right: depravity, impossibility, hatred, falsity, punishment, contrariness, emptiness, inflexibility, excess, diminution. Detail, Breviculum. Badische Landesbibliothek, code: St. Peter perg. 92. Kalrlsruhe.

All of its old tenants are still there, busy mincing and stirring the footage and tweets, tailoring the newsfeeds: wickedness, inactivity, ignorance, weakness, confusion, disaster, futility, nothingness, distortion, impossibility, hatred, falsity, punishment, contrariness, emptiness, inflexibility, excess, diminution.

And truth? Perhaps she is free and it is now we who are imprisoned in the flattened machinations of Llull’s truth-rescuing machine.

×