See Martin Gardner, “The Fourth Dimension,” in The Philosophy of Left and Right: Incongruent Counterparts and the Nature of Space, eds. James Van Cleve and Robert E. Frederick (New York: Springer, 1991), 61.
Quoted in Alexander Koyré, From the Closed World to the Infinite Universe (Baltimore: John Hopkins University Press, 1957), 245.
In later writings Kant came to espouse a different view, namely the one we usually identify with Kantian Idealism. The Kantian synthesis entailed a reconceptualization of the dichotomy between absolute and relational space over which Newton and Leibniz had contended, into the opposition real vs. ideal. Space, Kant argued, is absolute and independent from material bodies because it lacks concrete reality: space is a form of human perception, it is our subjective means of cognizing the world. Thus it is ideal (or mental) rather than real.
Gardner, “The Fourth Dimension,” 63.
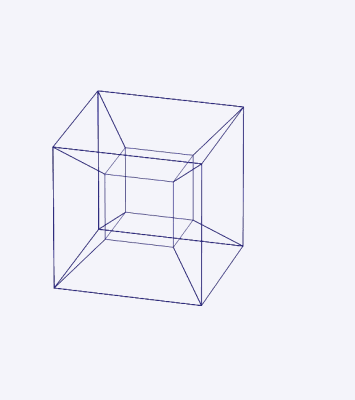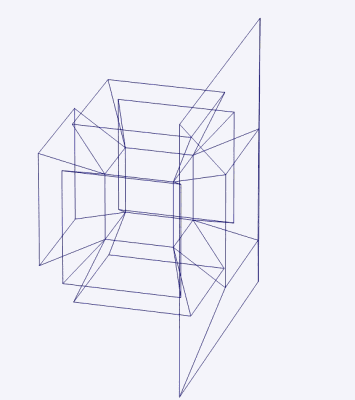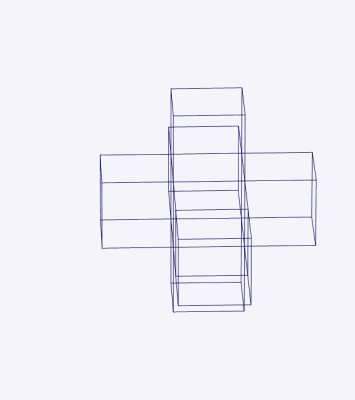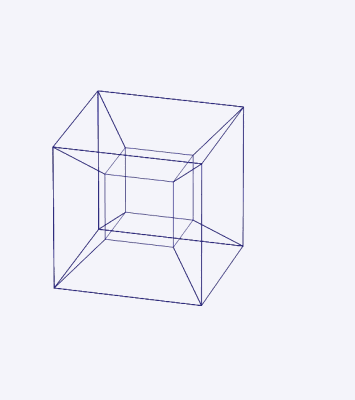
The dimension of a mathematical space is usually defined by the minimum number of coordinates necessary to specify a location in it: a cube, for instance, has dimension three, whereas a hypercube—the four-dimensional analogue of the cube—has dimension four. In ordinary language one is nevertheless tempted to say that a hypercube has four dimensions, which implies corporeality.
Hermann von Helmholtz, “On the Origin and Significance of the Axioms of Geometry,” Mind, Vol. 1, No. 3 (July 1876): 301–321.
The claim was made in the “Queries” appended to Newton’s Opticks. He later allegedly attempted to recall the whole edition.
Courtenay Grean Raia, “From ether theory to ether theology: Oliver Lodge and the physics of immortality,” Journal of the History of the Behavioral Sciences, Vol. 43, No. 1 (Winter 2007): 18–43.
Bruce J. Hunt, “Lines of Force, Swirls of Ether,” in From Energy to Information: Representation in Science and Technology, Art, and Literature, eds. Bruce Clarke and Linda Dalrymple Henderson (Stanford: Stanford University Press, 2002), 100.
Other observers included William Edward Weber, professor of physics; W. Scheibner, professor of mathematics; and the above-mentioned Gustave Theodore Fechner, professor of physics.
The Seybert Commission (1884–87) was an investigative committee created by the faculty of the University of Pennsylvania to scrutinize the claims of spiritists and mediums.
Linda Dalrymple Henderson, The Fourth Dimension and Non-Euclidian Geometry in Modern Art (Princeton: Princeton University Press, 1983), 28.
Stringham’s article was published in the American Journal of Mathematics.
It was Hinton who introduced the term “tesseract” for what is regularly known as the hypercube. The word combines the prefix τέσσᾰρᾰ, meaning “four,” and the word ἀκτίς, meaning “ray” (after which the radioactive element actinium was named). Each vertex of the tesseract would cast out a ray, able to pierce through interdimensional space.
Bernhard Riemann had also anticipated that gravity and electromagnetism were the effects of spatial distortions. Einstein would later add that the gravitational force is not a force per se, but a property of four-dimensional space-time.
For Kaluza, light can be explained as a vibration in the fifth dimension (after Einstein, the fourth would be described as time.) What became known as Kaluza-Klein theory is fundamental for string theory, which describes the properties of matter as gravitational vibrations (or strings).
Letter from Hiram Barton to Martin Gardner about Gardner’s review of Hinton’s work. The letter is reproduced in full here →
In Carroll’s world, where there are no absolute “Laws of Nature,” all sense of proportion (both literal and metaphorical) is lost and Alice finds it hard to keep her size constant. She also meets a caterpillar who is sitting on a mushroom while smoking a hookah, a phallic overkill which hints at the sexually charged imagery of everything oriental for Victorian audiences (algebra is derived from the Arab al jabr).
Carl B. Boyer, A History of Mathematics (Hoboken, NJ: Wiley, 1968), 18.
This slippage between the language of algebra and the language of geometry will create a belief in the reality of transcendental space. In the “Lion and the Unicorn” episode in Alice in Wonderland, Alice says she sees “nobody” coming down the road, to which the King replies, “I only wish I had such eyes … to be able to see nobody! And at that distance, too”—thus hypostatizing “nobody” into a proper noun. See Elizabeth Throesch, “Nonsense in the Fourth Dimension of Literature,” in Alice Beyond Wonderland, ed. Cristopher Hollingsworth (Iowa City: University of Iowa Press, 2009).
Bertrand Russell, Foundations of Logic, 1903–05 edition, eds. Alasdair Urquhart and Albert C. Lewis (London: Routledge, 1994), 579.
Henderson, The Fourth Dimension, 32.
Jean Clair, Sur Marcel Duchamp et la Fin de l’Art (Paris: Gallimard, 2000), 167.
See Susan C. Lawrence and Kae Bendixen, “His and Hers: Male and Female Anatomy in Anatomy Texts for U.S. Medical Students, 1890–1989,” Social Science & Medicine, Vol. 35, No. 7 (1992): 925–934 →
Ibid.
See Richard Wallace, Jack the Ripper: Light-Hearted Friend (Melrose, MA: Gemini Press, 1996).
Quoted in Henderson, The Fourth Dimension, 36.